1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
|
"""
目标：In this lab, you will implement linear regression with one variable to predict profits for a restaurant franchise.
问题陈述：
假设你是餐厅CEO，想要在不同城市开分店
想要把业务拓展到更高利润的城市
连锁店已经在各个城市开设了餐厅，并且你拥有来自城市的利润和人口数据
你还有餐厅候选城市的数据
"""
# 导包
import numpy as np
import matplotlib.pyplot as plt
import copy
import math
from utils import *
from public_tests import *
def cat_data():
"""
查看数据维度和形式等
"""
print("x_data数据类型：", type(x_train)) # <class 'numpy.ndarray'>
print("y_data数据类型：", type(y_train)) # <class 'numpy.ndarray'>
# 查看数据的维度
print("x_data的shape:", x_train.shape)
print("x_data的维度:", x_train.ndim)
print("数据集个数(m):", len(x_train))
# 可视化数据
plt.scatter(x_train, y_train, marker='x', c='r')
plt.title("Profits vs. Population per city")
plt.ylabel('Profit in $10000')
plt.xlabel('Population of City in 10000')
plt.show()
# 我们的目标就是建立线性回归model来fit这个data
def compute_cost(x, y, w, b):
"""
计算线性回归的代价函数
Args:
x (ndarray): Shape (m,) Input to the model (Population of cities)
y (ndarray): Shape (m,) Label (Actual profits for the cities)
w, b (scalar): Parameters of the model
Returns
total_cost (float): The cost of using w,b as the parameters for linear regression
to fit the data points in x and y
"""
# 训练集的个数
m = x.shape[0]
# You need to return this variable correctly
total_cost = 0
### START CODE HERE ###
cost_sum = 0
for i in range(m):
f_wb_i = w * x[i] + b
cost_i = (f_wb_i - y[i]) ** 2
cost_sum += cost_i
total_cost = (1 / (2 * m)) * cost_sum
### END CODE HERE ###
return total_cost
def compute_gradient(x, y, w, b):
"""
计算线性回归的梯度(也就是两个偏导数)
Args:
x (ndarray): Shape (m,) Input to the model (Population of cities)
y (ndarray): Shape (m,) Label (Actual profits for the cities)
w, b (scalar): Parameters of the model
Returns
dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
dj_db (scalar): The gradient of the cost w.r.t. the parameter b
"""
# Number of training examples
m = x.shape[0]
# You need to return the following variables correctly
dj_dw = 0 # 两个偏导数
dj_db = 0
### START CODE HERE ###
for i in range(m):
f_wb = w * x[i] + b # 线性回归模型
dj_dw_i = (f_wb - y[i]) * x[i] # f中对w的偏导
dj_db_i = f_wb - y[i] # f中对b的偏导
dj_db += dj_db_i
dj_dw += dj_dw_i
dj_dw = dj_dw / m
dj_db = dj_db / m
### END CODE HERE ###
return dj_dw, dj_db
def gradient_descent(x, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters):
"""
梯度下降的过程
Performs batch gradient descent to learn theta. Updates theta by taking
num_iters gradient steps with learning rate alpha
Args:
x : (ndarray): Shape (m,)
y : (ndarray): Shape (m,)
w_in, b_in : (scalar) Initial values of parameters of the model
cost_function: function to compute cost
gradient_function: function to compute the gradient
alpha : (float) Learning rate
num_iters : (int) number of iterations to run gradient descent
Returns
w : (ndarray): Shape (1,) Updated values of parameters of the model after
running gradient descent
b : (scalar) Updated value of parameter of the model after
running gradient descent
"""
# number of training examples
m = len(x)
# An array to store cost J and w's at each iteration — primarily for graphing later
J_history = []
w_history = []
w = copy.deepcopy(w_in) # avoid modifying global w within function
b = b_in
for i in range(num_iters):
# Calculate the gradient and update the parameters
dj_dw, dj_db = gradient_function(x, y, w, b) # 调用计算梯度的方法
# Update Parameters using w, b, alpha and gradient(同时更新)
w = w - alpha * dj_dw
b = b - alpha * dj_db
# Save cost J at each iteration
if i < 100000: # prevent resource exhaustion
cost = cost_function(x, y, w, b) # 计算代价
J_history.append(cost)
# Print cost every at intervals 10 times or as many iterations if < 10
if i % math.ceil(num_iters / 10) == 0:
w_history.append(w)
print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f} ")
return w, b, J_history, w_history # return w and J,w history for graphing
def draw_plot(w, b):
"""
画出图像
:param w:
:param b:
:return:
"""
m = x_train.shape[0]
predicted = np.zeros(m)
for i in range(m):
predicted[i] = w * x_train[i] + b # 计算出预测值
# Plot the linear fit
plt.plot(x_train, predicted, c="b")
# Create a scatter plot of the data.
plt.scatter(x_train, y_train, marker='x', c='r')
# Set the title
plt.title("Profits vs. Population per city")
# Set the y-axis label
plt.ylabel('Profit in $10,000')
# Set the x-axis label
plt.xlabel('Population of City in 10,000s')
plt.show()
def main():
# cat_data()
# 执行代价函数
# Compute cost with some initial values for paramaters w, b
# initial_w = 2
# initial_b = 1
# cost = compute_cost(x_train, y_train, initial_w, initial_b)
# print(type(cost))
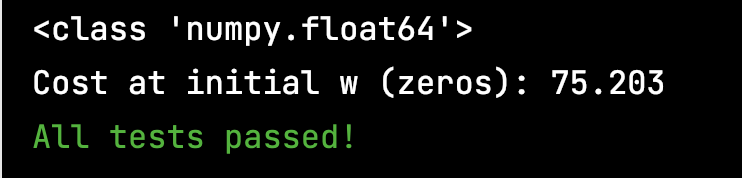
# print(f'Cost at initial w (zeros): {cost:.3f}')
# 调用测试：Public tests
# compute_cost_test(compute_cost)
# 在w和b不为0的情况下计算和展示代价函数和梯度
# test_w = 0.2
# test_b = 0.2
# tmp_dj_dw, tmp_dj_db = compute_gradient(x_train, y_train, test_w, test_b)
#
# print('Gradient at test w, b:', tmp_dj_dw, tmp_dj_db)
# initialize fitting parameters. Recall that the shape of w is (n,)
initial_w = 0.
initial_b = 0.
# some gradient descent settings
iterations = 1500
alpha = 0.01
w, b, _, _ = gradient_descent(x_train, y_train, initial_w, initial_b,
compute_cost, compute_gradient, alpha, iterations)
print("w,b found by gradient descent:", w, b)
draw_plot(w, b)
predict1 = 3.5 * w + b
print('For population = 35,000, we predict a profit of $%.2f' % (predict1 * 10000))
predict2 = 7.0 * w + b
print('For population = 70,000, we predict a profit of $%.2f' % (predict2 * 10000))
if __name__ == '__main__':
# 加载数据 x_train是城市人口(人口代表其值*10000)，y_train代表利润(有正负,值*$10000)
x_train, y_train = load_data()
main()
|
我们预测的餐厅利润就是$f_{w,b}(x^{(i)})$的值
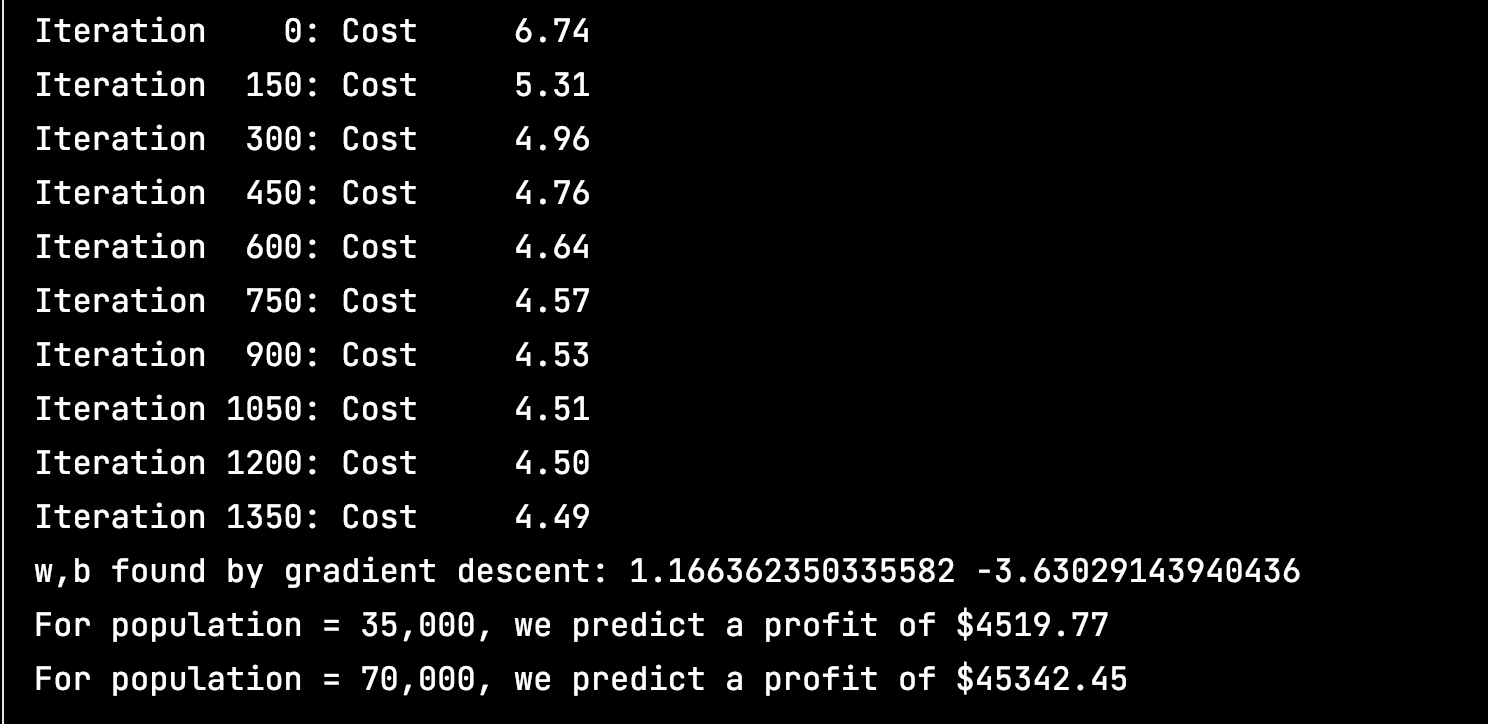
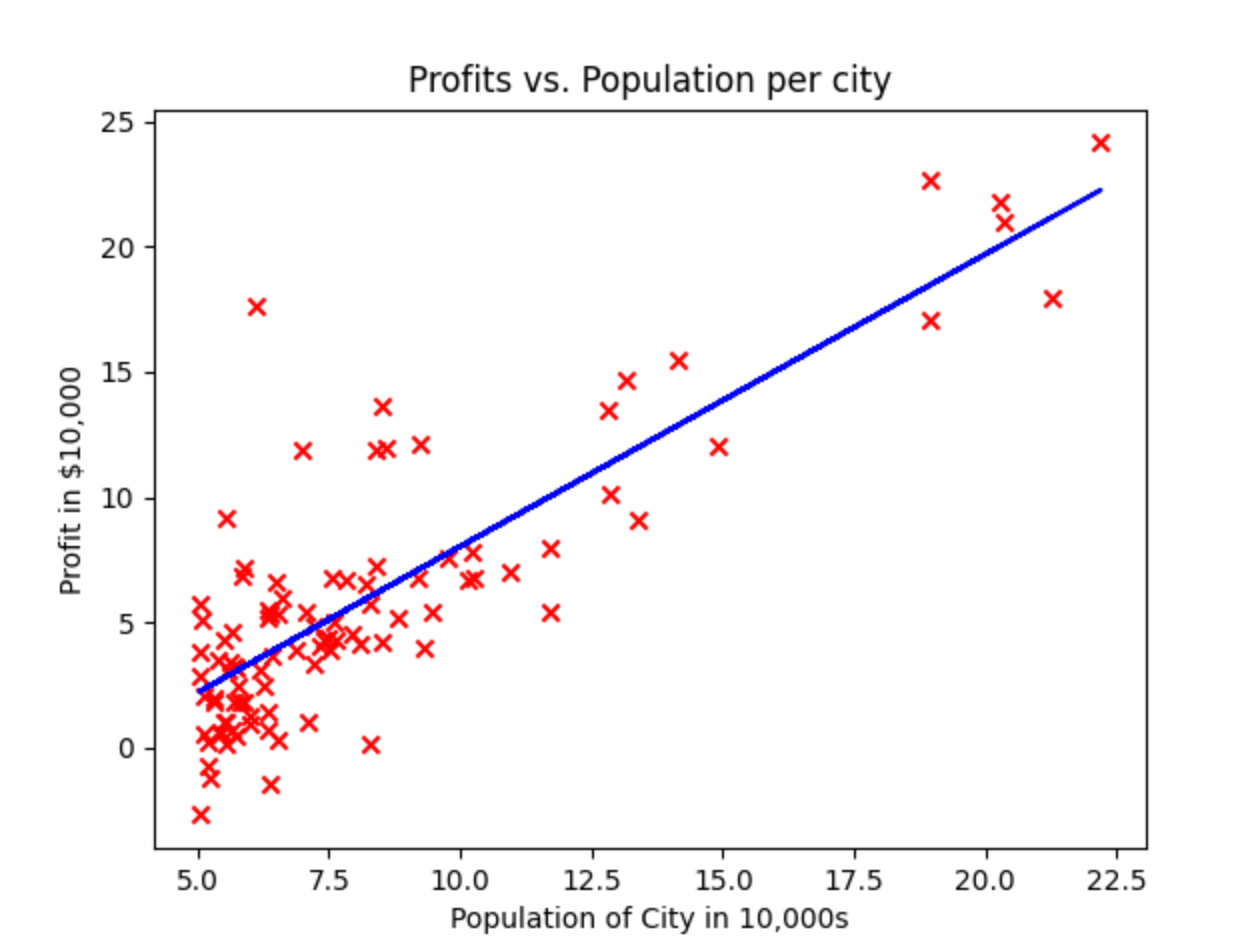可以看到最终的w和b可以用来进行预测