高偏差(high bias)和高方差(high variance)
本文主要参考别人的文章加入自己的话来帮助自己的理解,非原创哦
最近在学Andrew的Machine Learning课程,在学习欠拟合(under fitting)和过拟合(over-fitting接触到了高偏差(high bias)和高方差(high variance)的概念,很轻易的记住了:
- 过拟合–>高方差
- 欠拟合–>高偏差 的结论,但是对其中仍有许多不解,且Andrew举过他一个学生还是朋友的例子说高方差和高偏差需要很长时间去真正的理解,遂Google了一些文章帮助自己稍微理解这两个概念。
几个概念区分
模型 & 训练模型
我们每次使用训练集训练出来一个"模型"(其实应该叫做训练模型,因为每次更换训练集,训练出的“模型”并不一样,即各个训练模型被训练出来的参数(系数)是不一样的)
我们不可能得到用于训练这个模型的所有数据,也就无法训练出使模型y=ax+b理论上100%正确的参数,所以我们只能得到不同的训练模型。
参数(parameter) & 超参数(hyperparameter)
- 参数是被数据和算法训练出来的
- 而超参数(比如学习速率)不是被训练出来的,而是人为手工调整的。 调整超参数更像是一种艺术,而不是科学。
问题
既然我们永远无法训练出那个理想的模型,只能训练出训练模型,那么训练模型预测的结果和理论模型(即现实)的结果肯定就存在误差。我们肯定希望这个误差越小越好,并且将这个训练模型应用在其他数据集上的误差也是越小越好。那么问题来了,如果这个误差很大,我们该如何是好?
举例
该博主这个例子举得很好哈哈
假设我们要训练一个股票市场的模型,模型的目标是预测某支股票第2天的收益率,如果收益为正则买入,反之则卖出。我们的模型天天都想发财,它希望能准确预测每一天的涨跌,所以它关注的是第二天的收益,什么一年翻一倍之类的中长线策略它根本不关心。
- A模型:阅读了大量的巴菲特,彼得林奇等等各种大师的书籍和数据,它发现买入低估值股票的收益很可观,于是每天满仓杀入估值最低的N支股票。没过几天,它亏成了狗。它去质问股神,股神曰:“你把投资想象的太简单了,除了看估值,我还看很多其他指标”。
- B模型:吸取A模型的教训,它罗列了各种稀奇古怪的指标,最终惊喜的发现,模型成功的预测某支股票第二天的收益。万分惊喜下,它满仓杀入。第三天,第四天,第N天过去了,模型有时预测的准确,但大多时候谬之千里,还是亏成了🐶。
上面训练的2种模型,和我们期待的“神预测”模型有很大误差。我们要想减少预测误差,就要分析造成误差的原因。这里的误差包含:
- 偏差(bias):我们要预测第二天的收益,而估值指标经常用于长线投资,虽然每次预测都是信誓旦旦,但是模型从本质上就把目标搞错了。
- 方差(variance):过多的已知条件,导致模型无法给出确定的预测,预测结果和瞎蒙一样,给人的感觉是不靠谱。 无法消除的误差:我们都知道,完美预测第二天的情况,是不可能的。这样的误差难以消除,我们希望它越小越好,一般就忽略掉了。
所以,我们可以优化的误差=偏差+方差
打靶图
很经典的一张图(出处为第二个参考文献):
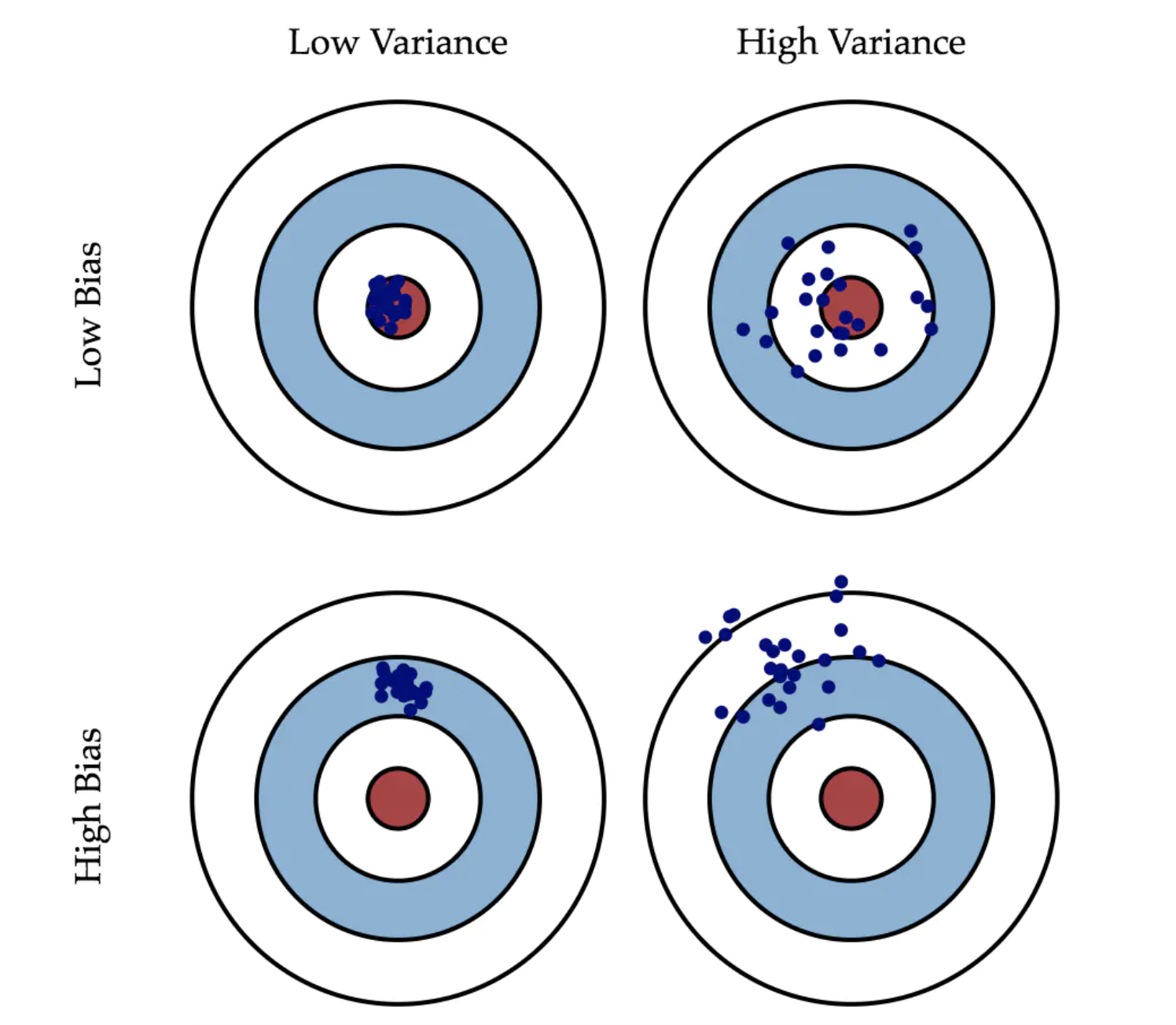
图中每一个蓝点,都代表了一个训练模型的预测数据,即根据不同的训练集训练出一个训练模型,再用这个训练模型作出一次预测结果。如果将这个过程重复N次,相当于进行了N次射击。 我们假设真实的函数关系是Y=f(x),而训练模型预测的结果是p(x),则
- 偏差错误:偏差是衡量预测值和真实值的关系。即N次预测的平均值(也叫期望值),和实际真实值的差距。所以偏差bias=E(p(x)) - f(x)。即bias是指一个模型在不同训练集上的平均表现和真实值的差异,用来衡量一个模型的拟合能力。
- 方差错误:方差用于衡量预测值之间的关系,和真实值无关。即对于给定的某一个输入,N次预测结果之间的方差。variance= E((p(x) - E(p(x)))^2)。这个公式就是数学里的方差公式,反应的是统计量的离散程度。只不过,我们需要搞清楚我们计算的方差的意义,它反映的是不同训练模型针对同一个预测的离散程度。即variance指一个模型在不同训练集上的差异,用来衡量一个模型是否容易过拟合
打靶图的理解:
-
高偏差,低方差: 每次射击都很准确的击中同一个位置,故极端的情况方差为0。只不过,这个位置距离靶心相差了十万八千里。对于射击而言,每次都打到同一个点,很可能是因为它打的不是靶心。对于模型而言,往往是因为模型过于简单,才会造成“准”的假象。提高模型的复杂度,往往可以减少高偏差。
-
高方差,低偏差: 是不是偏差越低越好?是不是低偏差时,方差也会低呢?通过对偏差的定义,不难发现,偏差是一个期望值(平均值),如果一次射击偏左5环,另一次射击偏右5环,最终偏差是0。但是没一枪打中靶心,所以方差是巨大的,这种情况也是需要改进的。方差越大,预测结果的分布越离散
如何解决
一般来说,当一个模型在训练集上的错误率比较高时,说明模型的拟合能力不够,偏差较高。 欠拟合(高偏差)的解决办法:
- 增加数据特征
- 提高模型负责度
- 减少正则化系数
当模型在训练集上的错误率比较低,但验证集上错误率比较高时,说明模型过拟合,方差比较高。 过拟合(高方差)的解决方法:
- 减低模型复杂度
- 加大正则化系数
- 引入先验知识
- 使用集成模型,即通过多个高方差模型的平均来降低方差
如何判断
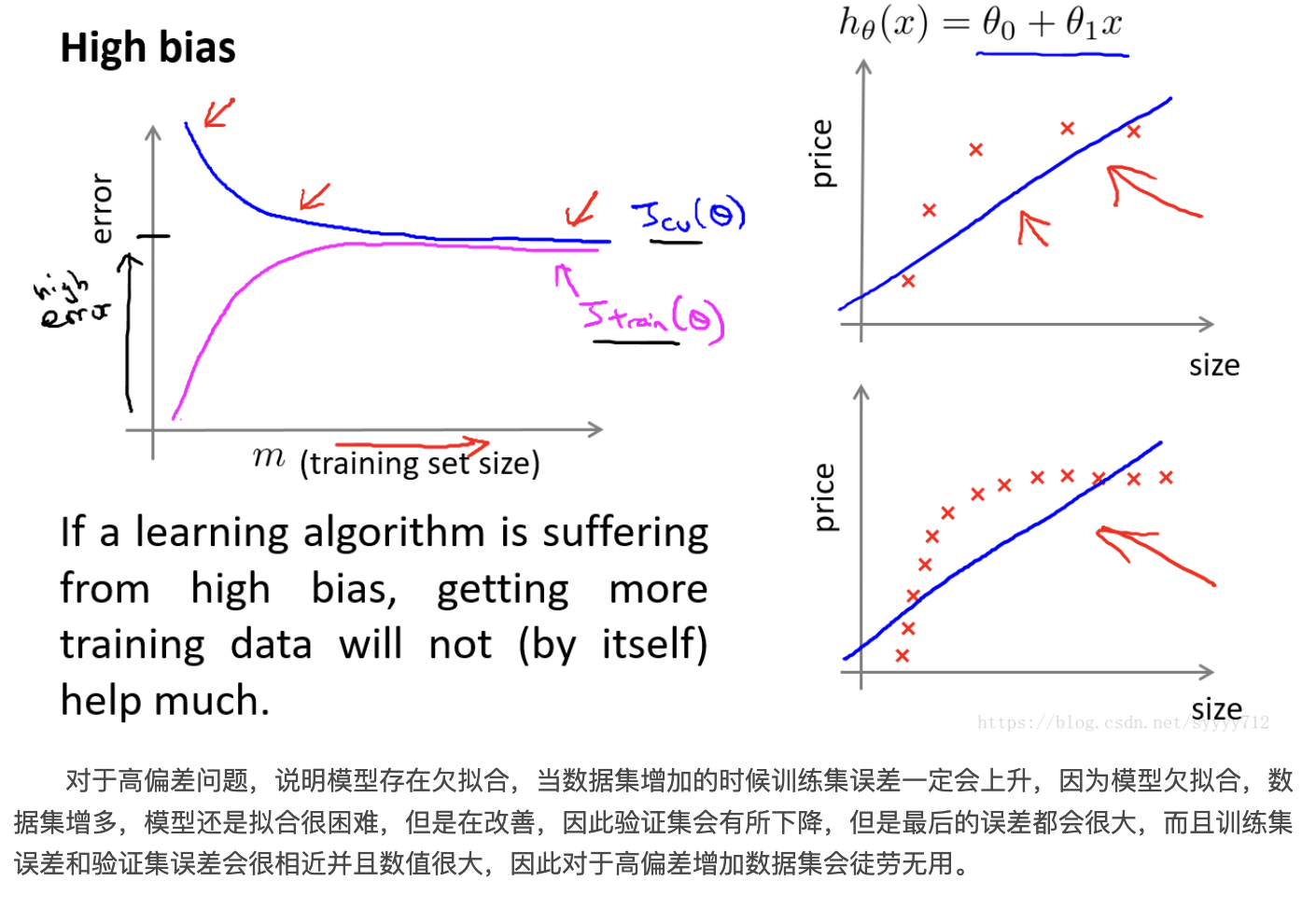
高偏差:
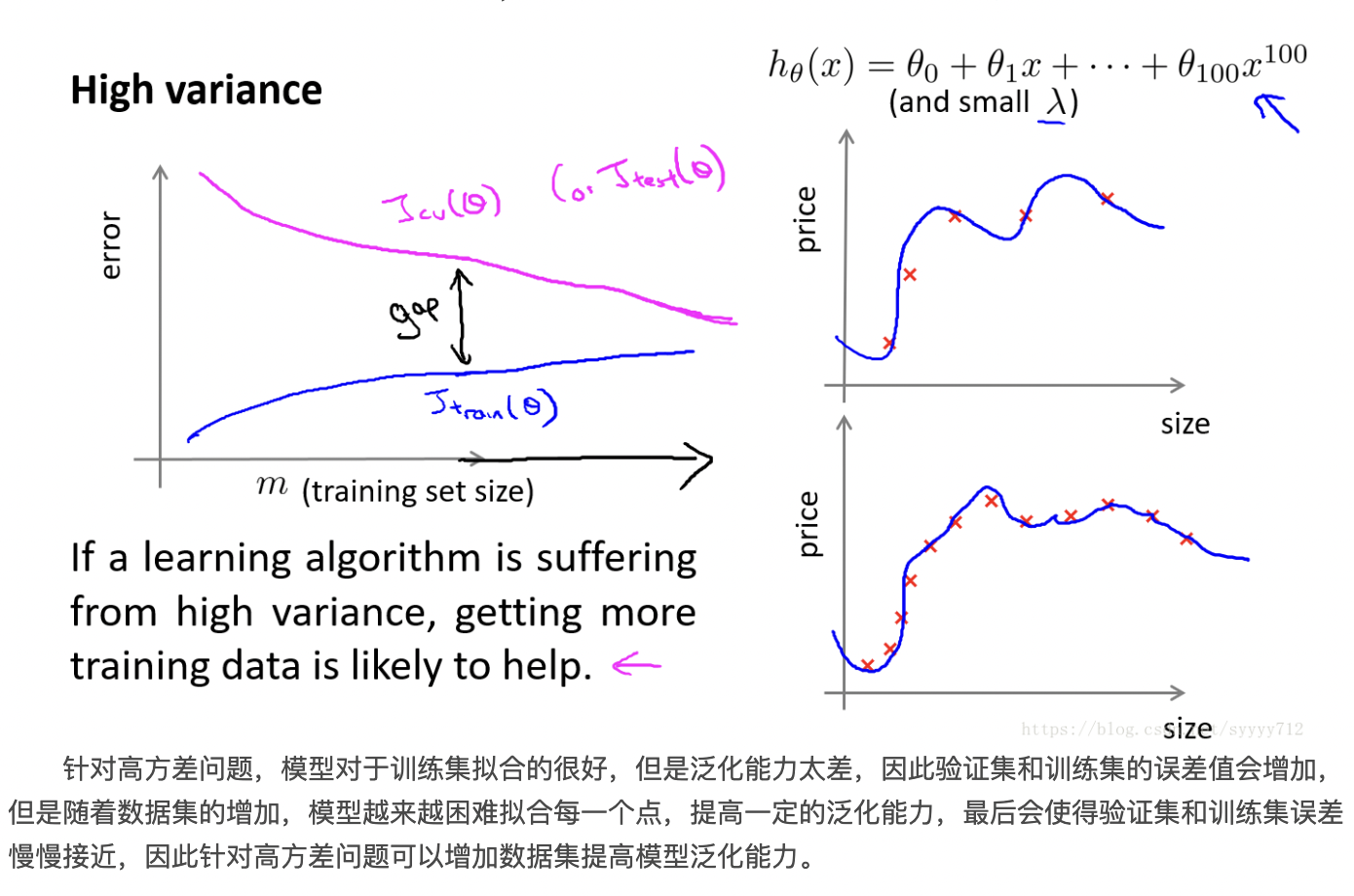
高方差:
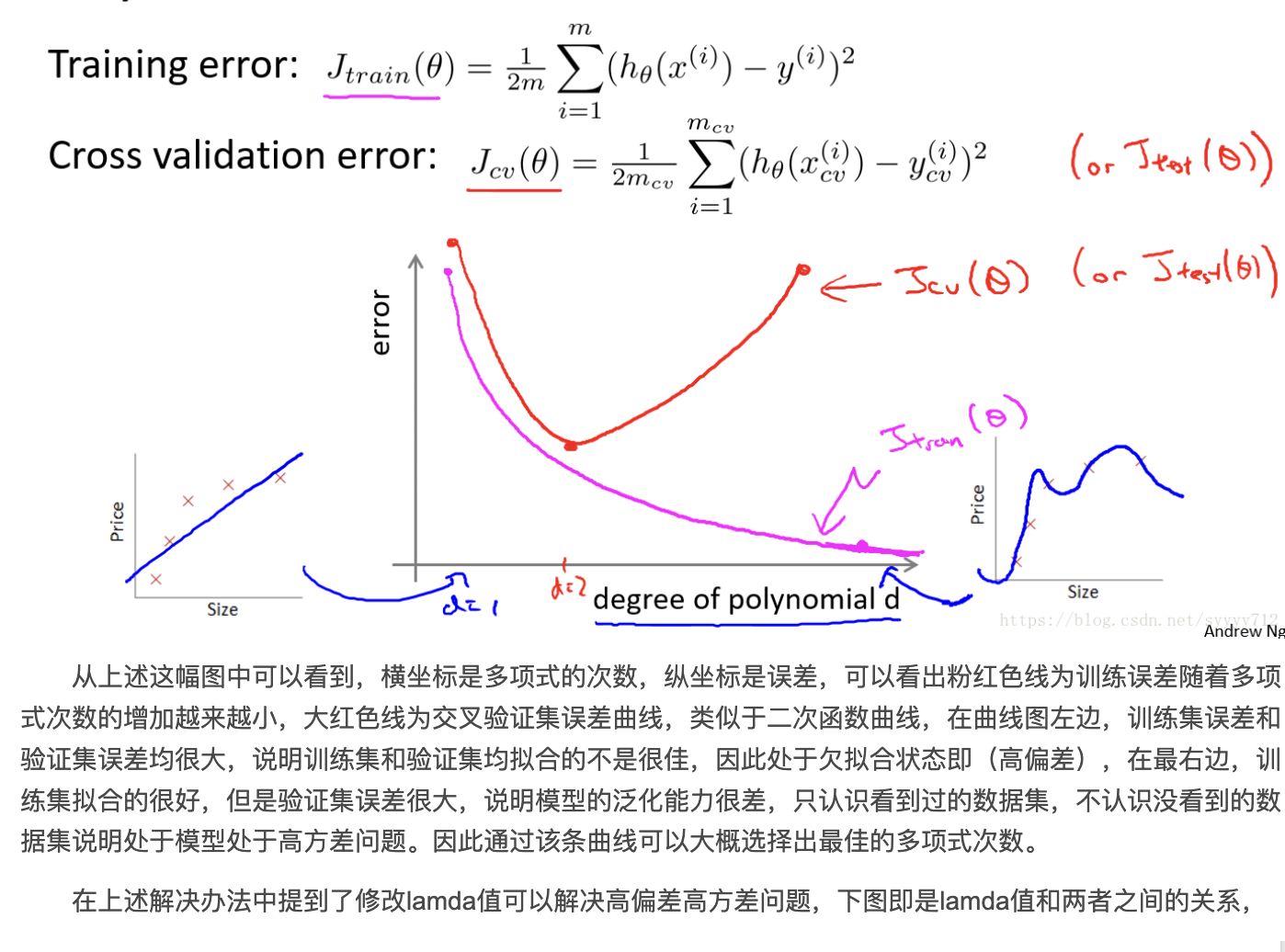
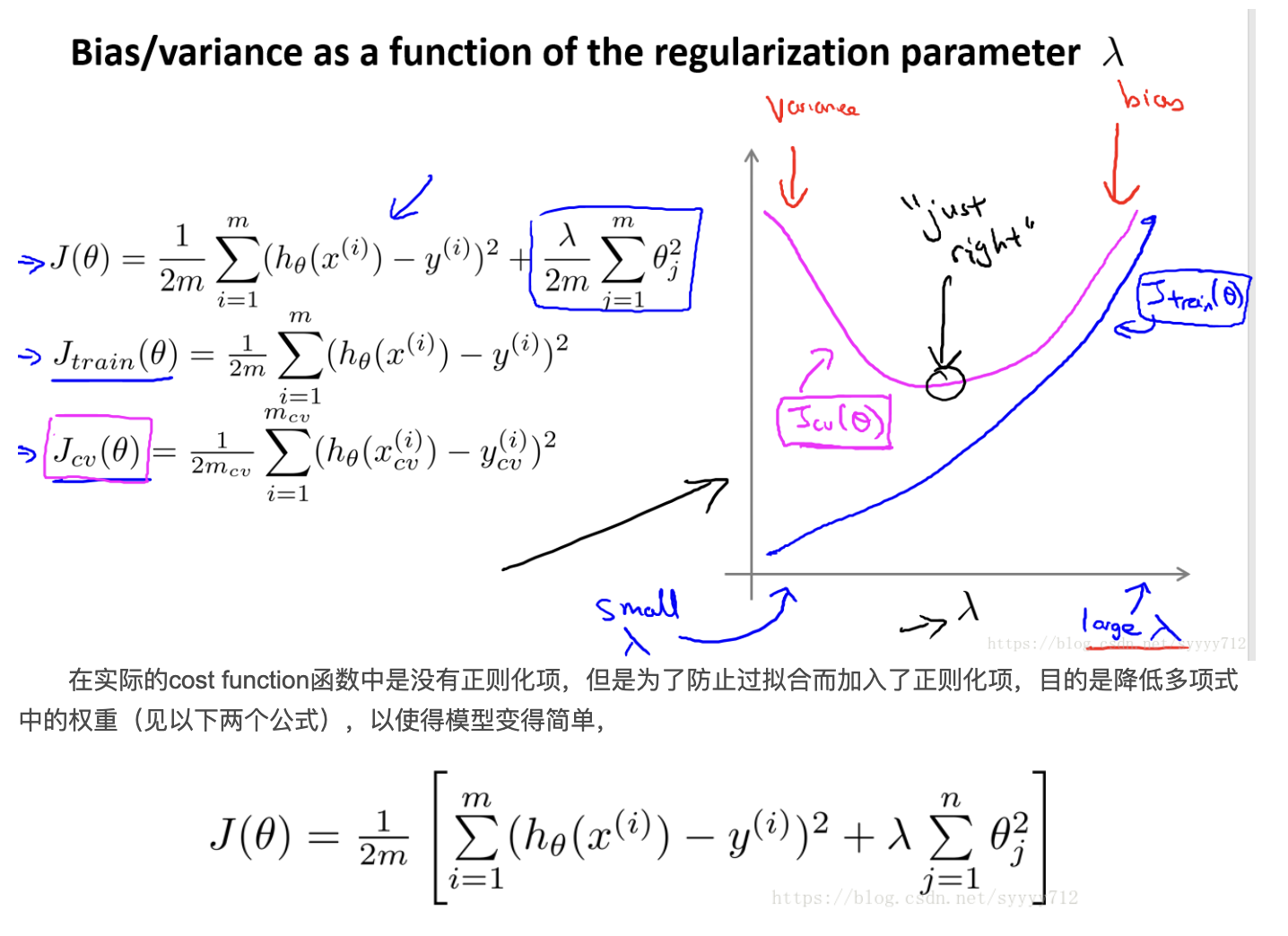
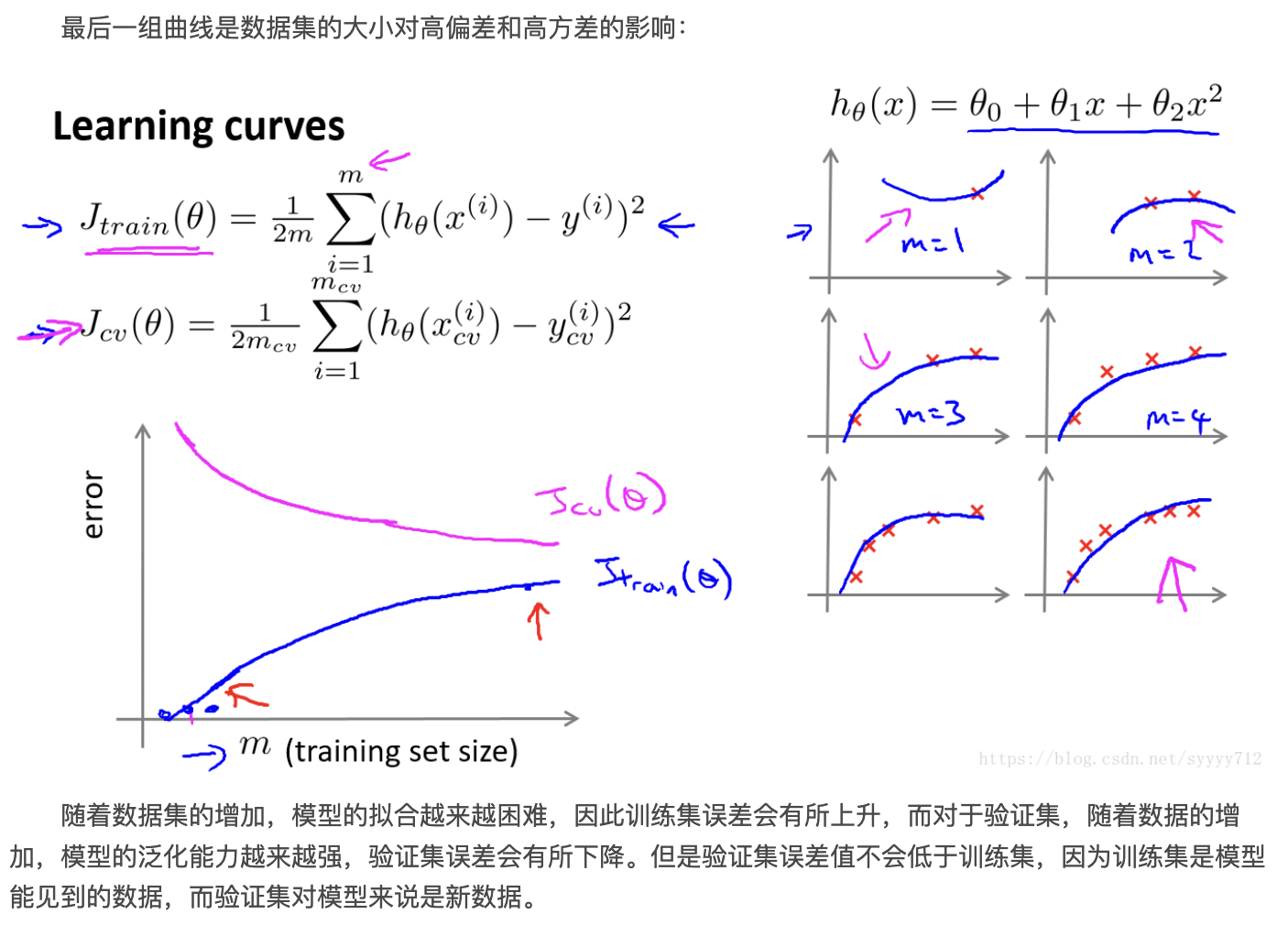
在上述解决办法中提到了修改lamda值可以解决高偏差高方差问题,下图即是lamda值和两者之间的关系:

参考文章
感谢博主的文章,受益匪浅: https://www.jianshu.com/p/a585d5506b1e http://scott.fortmann-roe.com/docs/BiasVariance.html