这几天看吴恩达深度学习作业时候,遇到了np.dot()、np.outer()、np.multiply()、*几个函数,记录一下
np.dot
1.如果处理的是一维数组,则得到的是两数组的內积(对应位置的元素相乘再相加)
参数的顺序不会影响结果
1
2
3
4
5
6
7
8
|
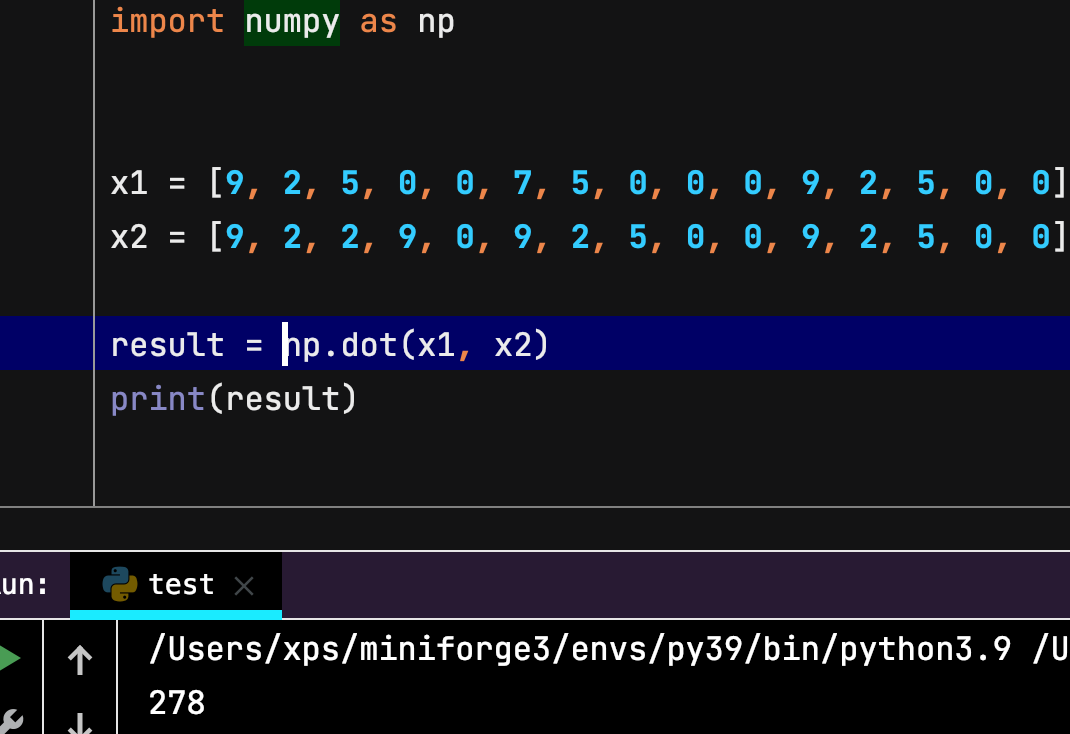
import numpy as np
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
result = np.dot(x1, x2)
print(result)
|

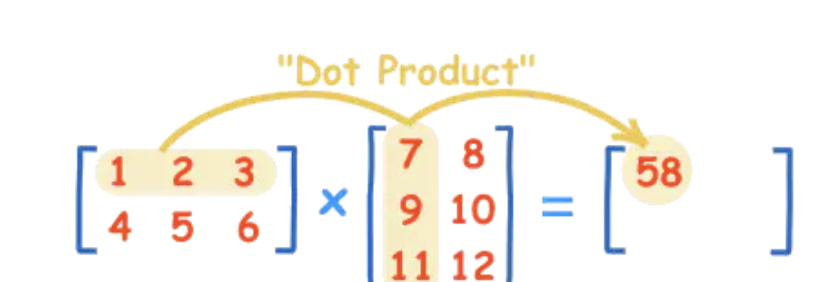
2.如果是二维数组(矩阵)之间的运算,则得到的是矩阵积(等同于矩阵乘法)
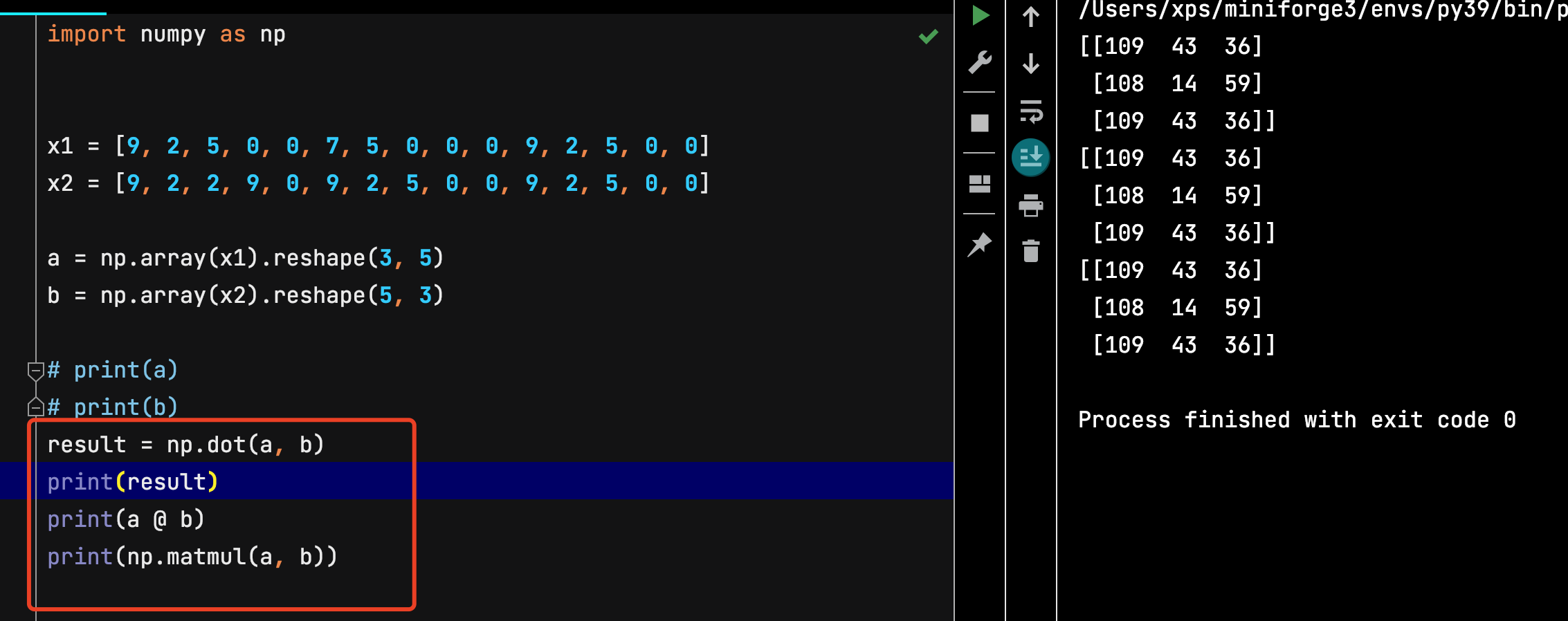
可以使用np.matmul 或者 a @ b 得到相同的答案
参数位置的不同会改变结果
注意:第一个矩阵的列和第二个矩阵的行的数字显得更才能计算
1
2
3
4
5
6
7
8
9
10
11
12
13
|
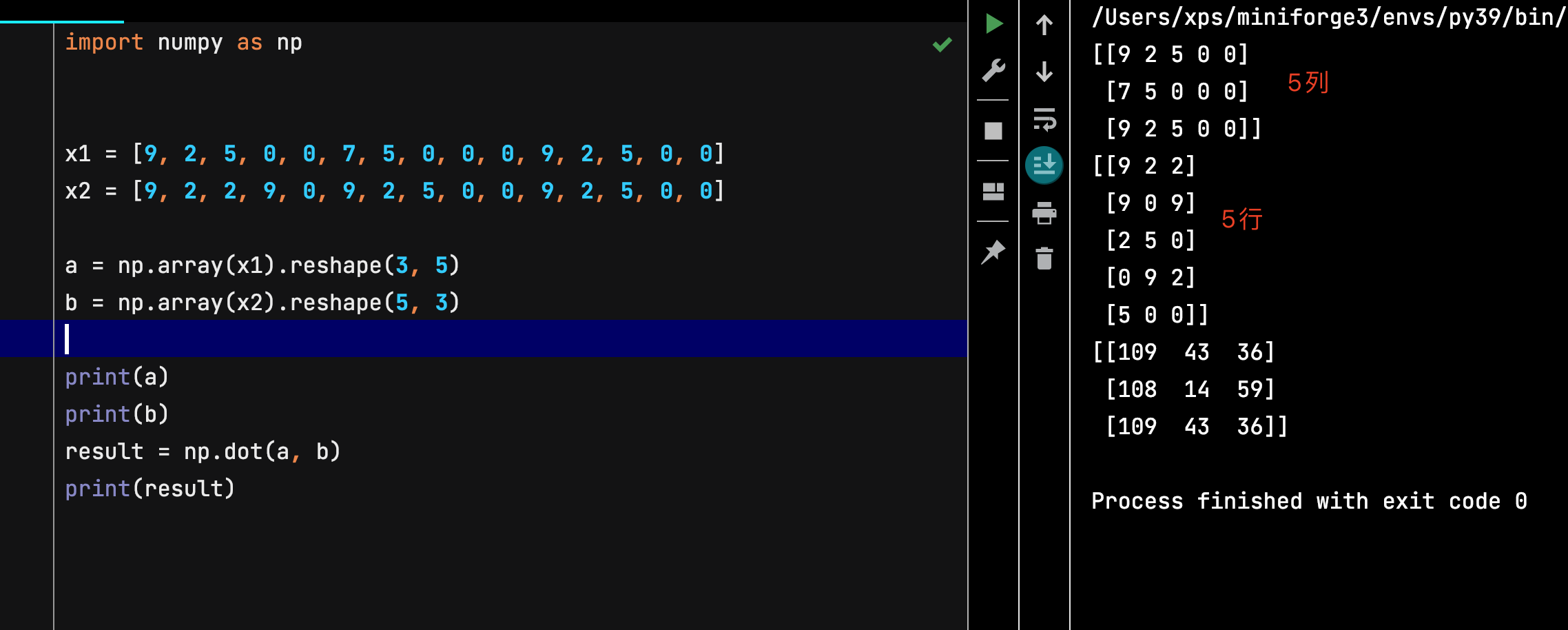
import numpy as np
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
a = np.array(x1).reshape(3, 5)
b = np.array(x2).reshape(5,3)
print(a)
print(b)
result = np.dot(a, b) # a.dot(b) 与 np.dot(a,b)效果相同
print(result)
|



3.如果 a 或者 b 中有一个是标量的,效果等价于np.multiply ,可以使用 multiply(a,b) 或者 a * b 也可以
参数位置不会改变答案
使用multiply或者 * 也可以
1
2
3
4
5
6
7
8
9
10
11
12
|
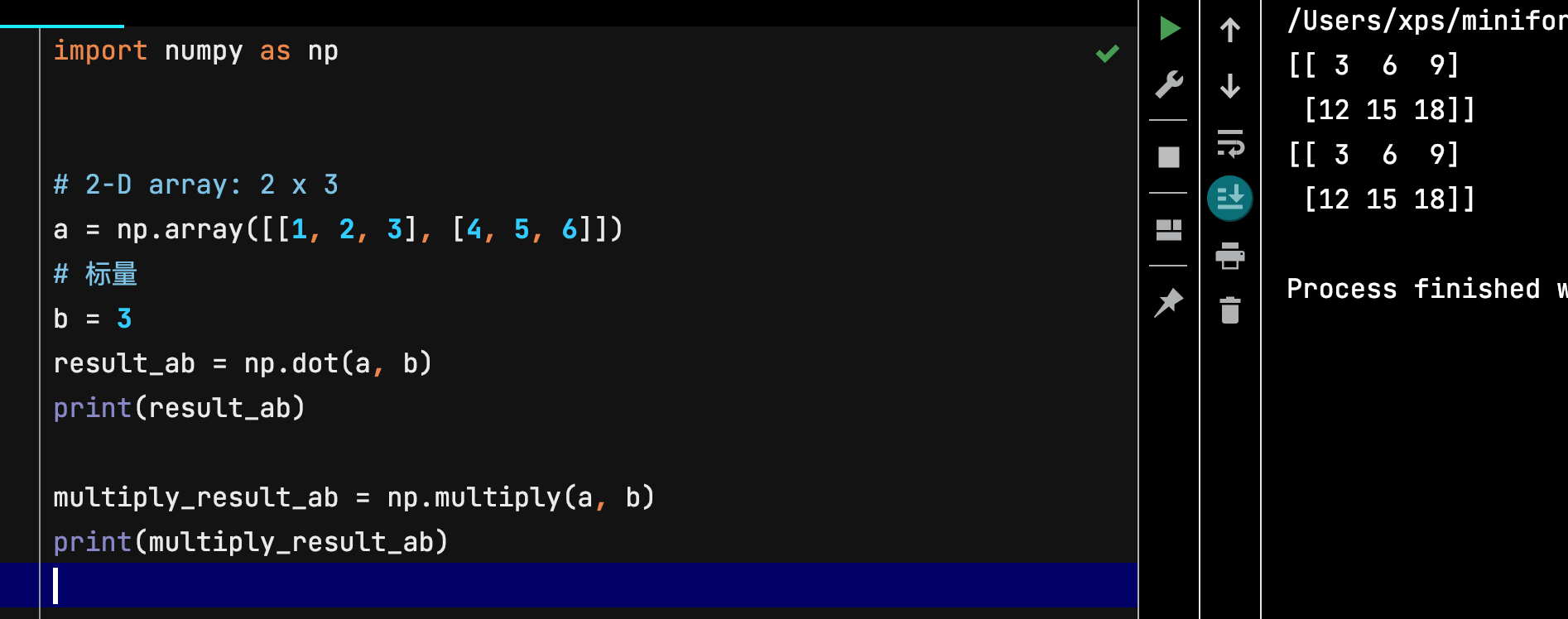
import numpy as np
# 2-D array: 2 x 3
a = np.array([[1, 2, 3], [4, 5, 6]])
# 标量
b = 3
result_ab = np.dot(a, b)
print(result_ab)
multiply_result_ab = np.multiply(a, b)
print(multiply_result_ab)
|

np.outer
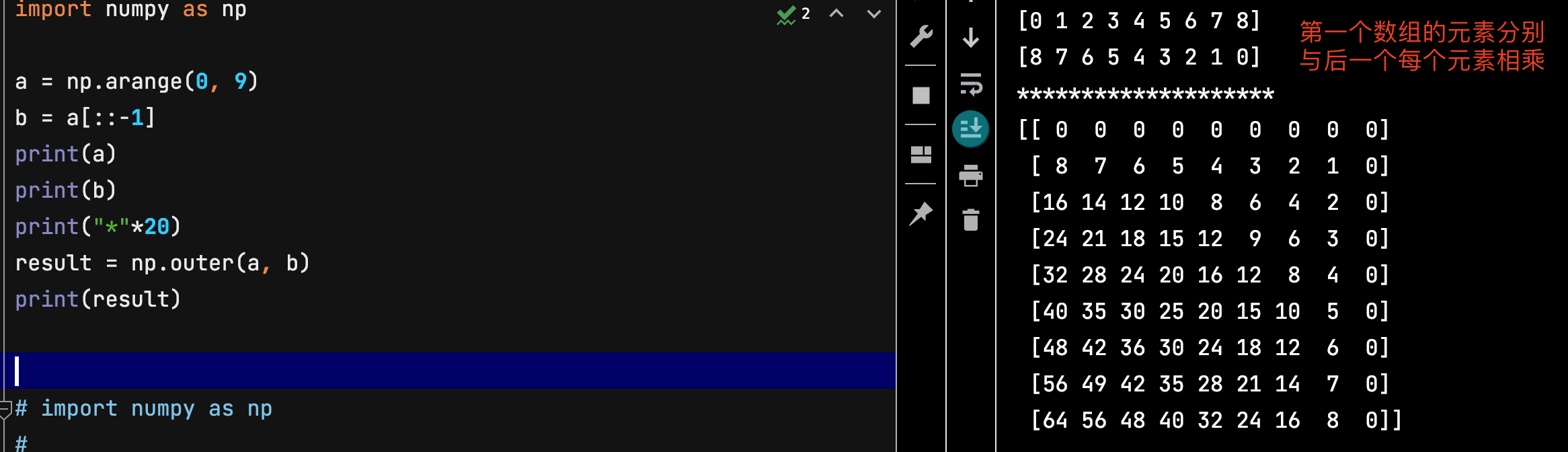
表示的是两个向量相乘,拿第一个向量的元素分别与第二个向量所有元素相乘得到结果的一行
1.数组
1
2
3
4
5
6
|
import numpy as np
a = np.arange(0,9)
b = a[::-1]
result = np.outer(a,b)
print(result)
|

2.矩阵
1
2
3
4
5
|
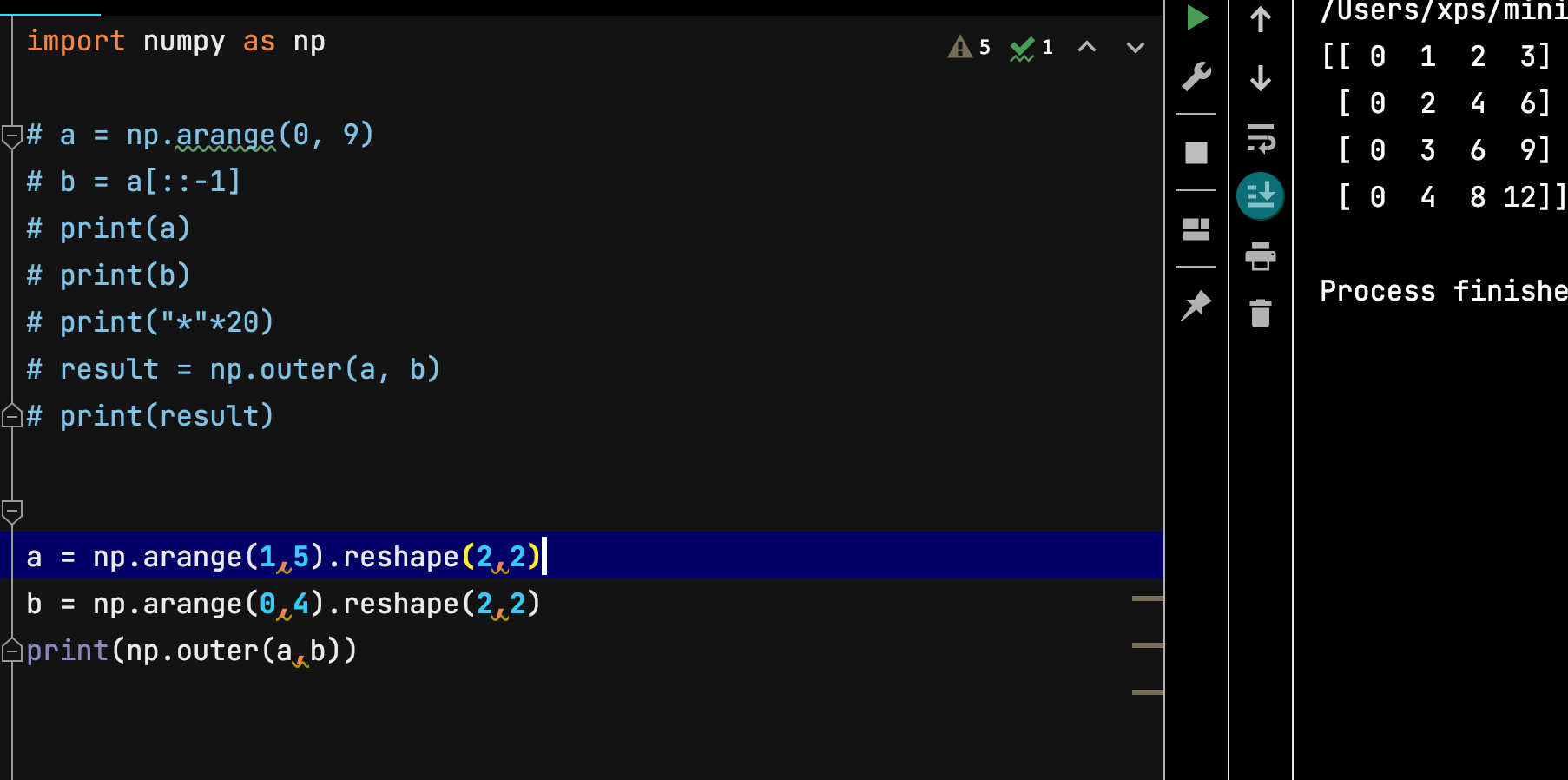
import numpy as np
a = np.arange(1,5).reshape(2,2)
b = np.arange(0,4).reshape(2,2)
np.outer(a,b)
|

np.multiply
表示的是数组和矩阵对应位置相乘,输出和输出的结果shape一致
1.数组
1
2
3
4
5
6
|
import numpy as np
a = np.arange(0,9)
b = a[::-1]
result = np.multiply(a,b)
print(result)
|

2.矩阵
1
2
3
4
5
6
|
import numpy as np
a = np.arange(1,5).reshape(2,2)
b = np.arange(0,4).reshape(2,2)
print(np.multiply(a,b))
|

*
1.对数组执行的是对应位置相乘
1
2
3
4
5
|
import numpy as np
a = np.arange(0,9)
b = a[::-1]
print(a*b)
|

2.对矩阵执行的是矩阵相乘
1
2
3
4
5
|
import numpy as np
a = np.arange(1,5).reshape(2,2)
b = np.arange(0,4).reshape(2,2)
print(a * b)
|

Note
- 对于array对象,*和np.multiply函数代表的是数量积,如果希望使用矩阵的乘法规则,则应该调用np.dot和np.matmul函数。
- 对于matrix对象,*直接代表了原生的矩阵乘法,而如果特殊情况下需要使用数量积,则应该使用np.multiply函数。
比较两幅图的不同:


题外话
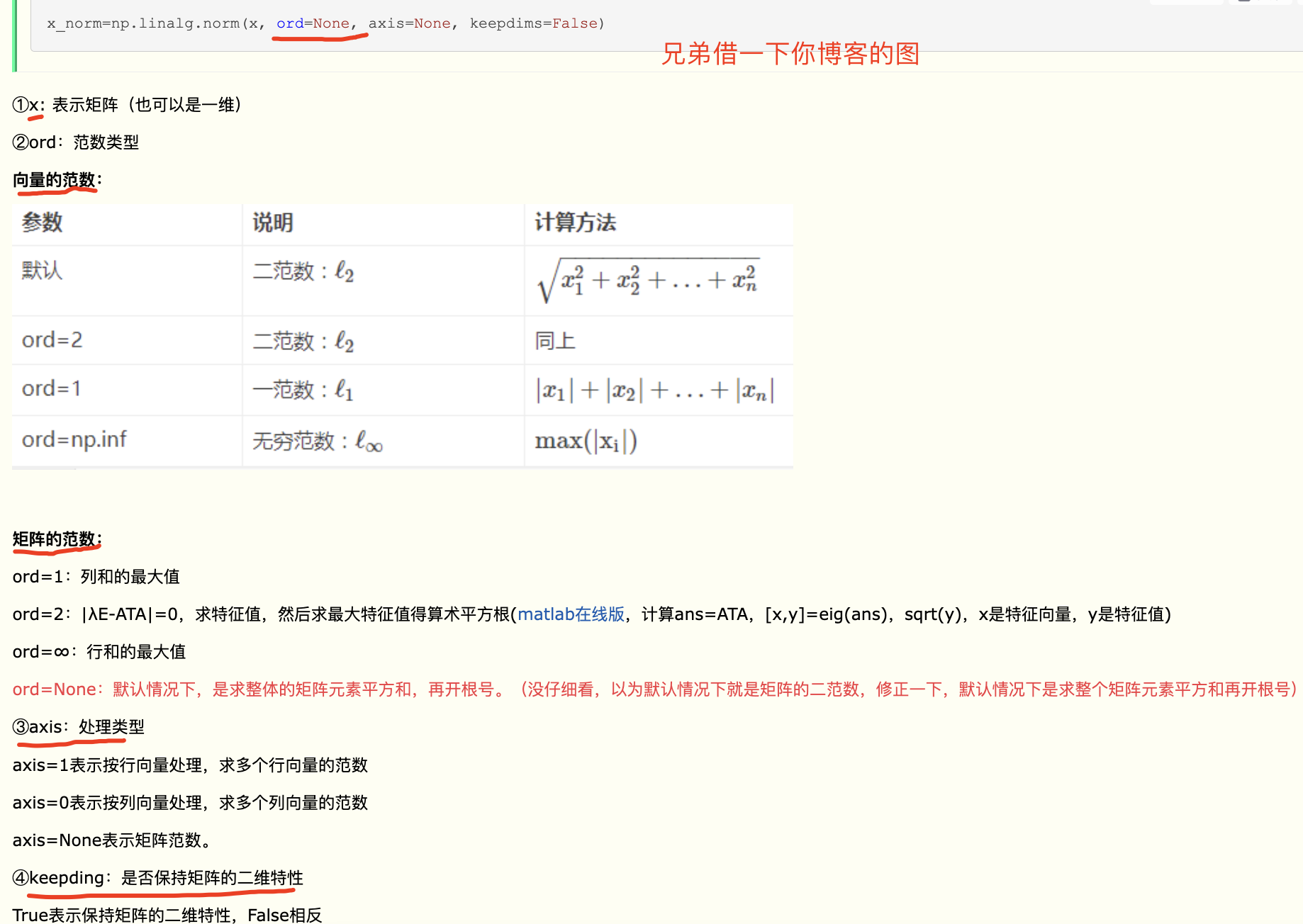
另外,遇到了一个求范数的函数:np.linalg.norm
np.linalg.norm就是元素平方求和之后开根号
函数的参数:
 默认参数
默认参数ord=None,axis=None,keepdims=False






 默认参数
默认参数