LeNet
1989年提出的

- 是早期成功的神经网络
- 先使用卷积层来学习图片空间信息
- 然后使用全连接层转换到类别空间
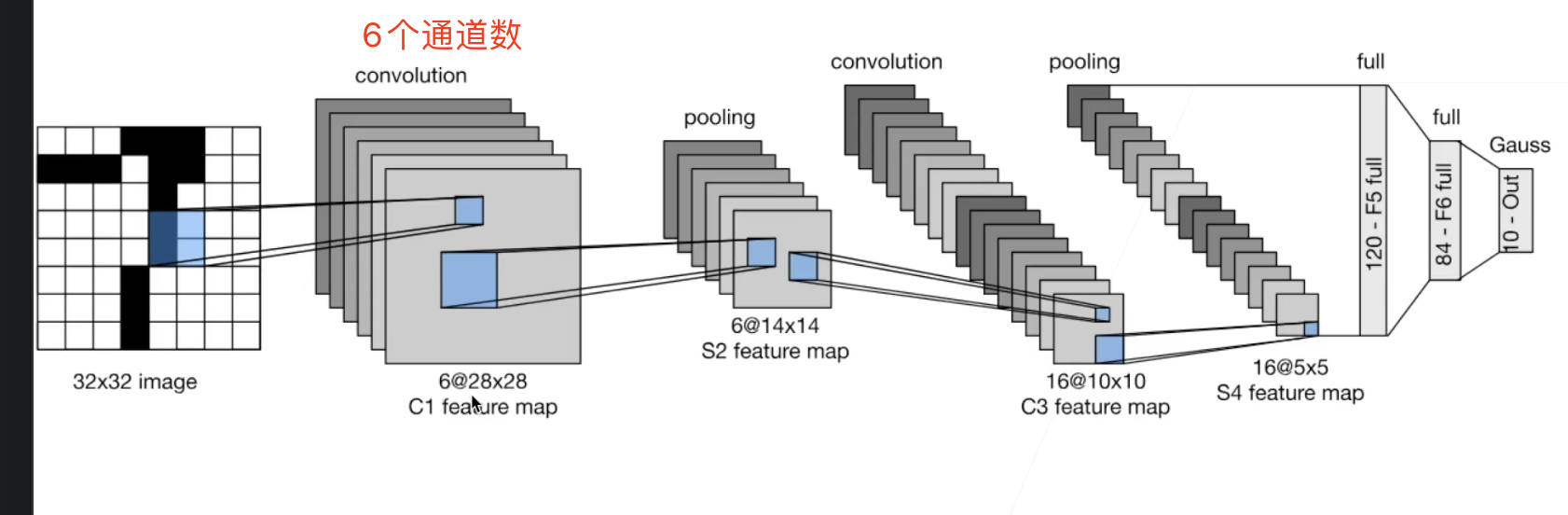
- LeNet交替使用卷积层和最大池化层后接全连接层来进行图像分类。
LeNet分为卷积层块和全连接层快两部分:
卷积层块里的基本单位是卷积层后接最大池化层:卷积层用来识别图像里的空间模式,如线条和物体局部,之后的最大池化层则用来降低卷积层对位置的敏感性。卷积层块由两个这样的基本单位重复堆叠构成。
卷积层块的输出形状为(批量大小, 通道, 高, 宽)。当卷积层块的输出传入全连接层块时,全连接层块会将小批量中每个样本变平(flatten)。也就是说,全连接层的输入形状将变成二维,其中第一维是小批量中的样本,第二维是每个样本变平后的向量表示,且向量长度为通道、高和宽的乘积。全连接层块含3个全连接层。它们的输出个数分别是120、84和10,其中10为输出的类别个数。
 其中形状是第一列输入的image的形状大小进行计算的
其中形状是第一列输入的image的形状大小进行计算的
网络实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
import torch
from torch import nn
from d2l import d2ltorch as d2l
class Reshape(torch.nn.Module):
def forward(self, x):
return x.view(-1, 1, 28, 28)
net = torch.nn.Sequential(
Reshape(),
# 原始图片为32*32 reshape为28*28后 需要进行2的填充
# 这里填充的目的是为了防止边缘信息被剪掉
nn.Conv2d(1,6,kernel_size=5,padding=2),
# 激活函数
nn.Sigmoid(),
# 卷积核为2 步幅为2 的均值池化层
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Conv2d(6,16,kernel_size=5),
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2,stride=2),
# 展平层,然后开始全连接层
nn.Flatten(),
nn.Linear(16*5*5,120),
nn.Sigmoid(),
nn.Linear(120,84),
nn.Sigmoid(),
nn.Linear(84,10)
# 我们对原始模型做了⼀点小改动,去掉了最后⼀层的⾼斯激活
)
|
这里可以预先检查一下,输入输出是否合理:
1
2
3
4
5
6
|
X = torch.rand(size=(1,1,28,28),dtype=torch.float32)
for layer in net:
X = layer(X)
# \t相当于tab按键
print(layer.__class__.__name__,'output shape: \t',X.shape)
# 尝试用X进行试验,可以看出每层输出的维度,这样也可以使得输入输出按照自己需求来
|
或者下面这样写:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5), # 16层厚
nn.Sigmoid(),
nn.MaxPool2d(2, 2)
)
self.fc = nn.Sequential(
nn.Linear(16*4*4, 120), # 这里其实还是进行一个卷积操作,通过120个5*5的卷积使得图像变为120*1*1
nn.Sigmoid(),
nn.Linear(120, 84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1)) # 卷积层和全连接层之间需要调整维度
return output
net = LeNet()
|
- 在整个卷积块中,与上⼀层相⽐,每⼀层特征的⾼度和宽度都减小了。
- 第⼀个卷积层使⽤2 个像素的填充,来补偿5X5 卷积核导致的特征减少。
- 相反,第⼆个卷积层没有填充,因此⾼度和宽度都减少了4 个像素。随着层叠的上升,通道的数量从输⼊时的1 个,增加到第⼀个卷积层之后的6 个,再到第⼆个卷积层
之后的16 个。
- 同时,每个汇聚层的⾼度和宽度都减半。最后,每个全连接层减少维数,最终输出⼀个维数与结果分类数相匹配的输出。
数据加载:使用Fashion-MNIST作为训练数据集
1
2
3
4
5
|
# 数据加载
batch_size = 256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)
# iter(train_iter).__next__()[0].shape
|
评估函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
# 因为卷积神经网络计算比多层感知机要复杂,建议使用GPU来加速计算
# 对评估函数进行GPU的实现
def evaluate_accuracy_gpu(net,data_iter,device = None):
"""使用GPU进行计算"""
# isinstance函数 用于判别
# 用于选择第一个设备
if isinstance(net,torch.nn.Module):
net.eval()
if not device:
device = next(iter(net.parameters())).device
# 正确预测的数量,总预测的数量
metric = d2l.Accumulator(2)
for X,y in data_iter:
# 如果x是list,那么把设备都加进去
if isinstance(X,list):
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
# 返回准确率、y的元素个数
metric.add(d2l.accuracy(net(X),y), y.numel())
return metric[0]/metric[1] # 正确的/个数
|
训练:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
def train_ch6(net,train_iter,test_iter,num_epochs,lr,device):
"""Gpu 训练模型"""
# 权重初始化函数
def init_weights(m):
if isinstance(m,nn.Linear) or isinstance(m,nn.ConstantPad2d):
nn.init.xavier_uniform_(m.weight) # xavier_uniform_初始化函数
# 应用权重分配
net.apply(init_weights)
print("traing on",device)
# 模型构建好后整体进行迁移
net.to(device)
optimizer = torch.optim.SGD(net.parameters(),lr = lr)
# optimizer = torch.optim.Adam(net.parameters(),lr = lr)
loss = nn.CrossEntropyLoss()
# 该函数主要用于动画展示
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
# epoch指的是整体数据需要循环十遍
for epoch in range(num_epochs):
# 训练损失之和,训练准确率之和,范例数
metric = d2l.Accumulator(3)
net.train()
# 标准循环
for i, (X, y) in enumerate(train_iter):
# 以batch_size大小进行训练
timer.start()
# 梯度归零
optimizer.zero_grad()
# 输入输出放入GPU
X, y = X.to(device), y.to(device)
# 正向操作
y_hat = net(X)
# 计算损失
l = loss(y_hat, y)
# 计算梯度
l.backward()
# 迭代
optimizer.step()
# 以下部分主要用于输出一些指标
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = evaluate_accuracy_gpu(net,test_iter)
animator.add(epoch + 1, (None, None, test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, 'f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec 'f'on {str(device)}')
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# 也可以尝试学习率采用0.001,训练算法使用Adam算法
|
可以访问这个网址更直观看到其过程:https://www.cs.ryerson.ca/~aharley/vis/conv/
尺寸变化
卷积之后尺寸的变化:
若图像为正方形:设输入图像尺寸为WxW,卷积核尺寸为FxF,步幅为S,Padding使用P,经过该卷积层后输出的图像尺寸为NxN:
$$
(W = \frac{W+2P-F}{S} + 1, H = \frac{H+2P-F}{S} + 1)
$$
池化之后:
设输入图像尺寸为WxH,其中W:图像宽,H:图像高,D:图像深度(通道数),卷积核的尺寸为FxF,S:步长(步长S就等于池化核的尺寸)
$$
W = \frac{W-F}{S} + 1,
H = \frac{H-F}{S} + 1,
$$
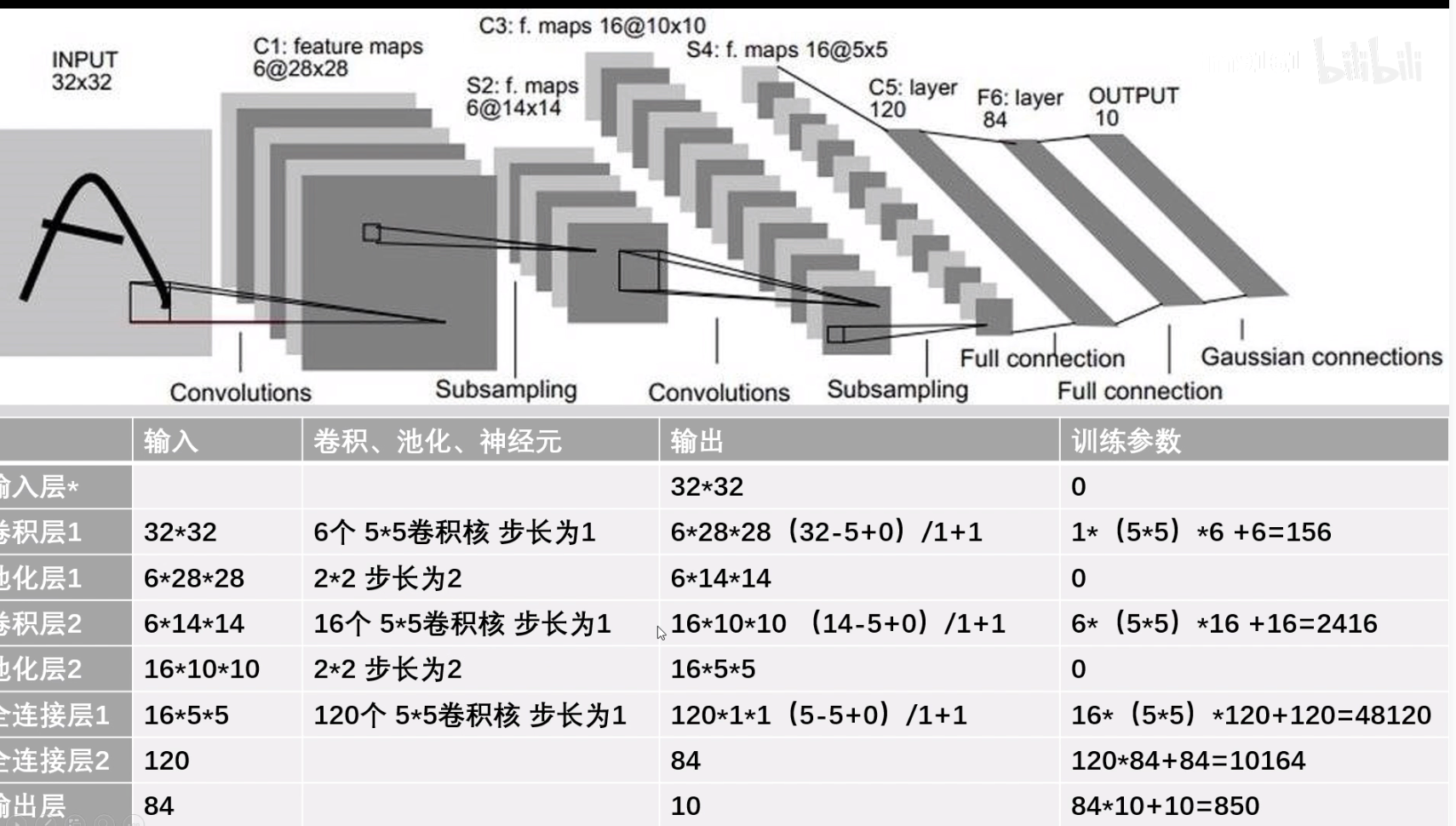 其中形状是第一列输入的image的形状大小进行计算的
其中形状是第一列输入的image的形状大小进行计算的